Compreensão & Prática

27/11/2013

Área do paralelogramo

O paralelogramo é um polígono que possui quatro lados, sendo que os segmentos paralelos possuem medidas iguais. Como todo quadrilátero, a soma dos ângulos internos é de 360º. Possui duas diagonais que se cruzam no ponto médio e os ângulos opostos possuem medidas iguais. Exemplo de um paralelogramo:

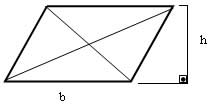
A fórmula usada para calcular a área de um paralelogramo é A = b x h (b: base e h: altura), sendo que a altura é perpendicular a base.

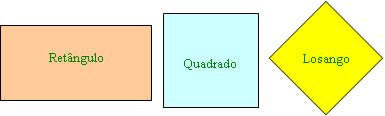
Retângulo: possui os quatro ângulos com medidas iguais, cada um medindo 90º e os lados paralelos opostos iguais.

Losango: possui os quatro lados com medidas iguais, ângulos opostos iguais, sendo dois ângulos agudos (medida menor que 90º) e dois ângulos obtusos (medida maior que 90º), lados paralelos entre si.

Quadrado: possui quatro lados com medidas iguais e os quatro ângulos com medidas iguais a 90º cada um.

Área do retângulo e do quadrado

Marcinha mora em uma casa que possui uma enorme área coberta. O pai de Marcinha resolveu colocar cerâmica na área. O pedreiro contratado para realizar a obra mediu a área e disse que ela tem a forma retangular com as seguintes dimensões: 9 metros de largura e 12 metros de comprimento, totalizando uma área de 108 metros quadrados (m²). Veja a ilustração da área:

Se o pai de Marcinha resolver comprar blocos de piso no formato quadrado, de 1 metro de largura e 1 metro de comprimento, ele precisará de pelo menos 108 blocos, pois cada um deles tem 1 metro quadrado (m²) de área e a superfície total da área coberta é de 108 metros quadrados (m²).

A área do quadrado e do retângulo é calculada multiplicando a medida do comprimento pela medida da largura. Todas as medidas devem estar na mesma unidade de comprimento. Veja a superfície da área com os blocos de cerâmica enumerados com dimensões de 1 metro de comprimento e 1 metro de largura.

Foram utilizados 108 blocos de cerâmica para cobrir toda a superfície da área.

Importante: O metro quadrado (m²) equivale à superfície ocupada por 1 quadrado de 1 metro de lado.

Após cobrir toda a superfície da área, o pai de Marcinha pretende trocar todo o piso da sala de vídeo da casa. As dimensões da sala são 6 metros de comprimento e 4 metros de largura.

A partir dessas dimensões conclui-se que a sala possui 24 metros quadrados de área (6m x 4m).

Área do losango

Losango é uma figura plana conhecida como quadrilátero, possuindo assim duas diagonais. O seu diferencial com relação às outras figuras que possuem 4 lados é que as suas diagonais cruzam perpendicularmente, ou seja, no ponto em comum das duas diagonais forma um ângulo de 90º.

Portanto, a área do losango poderá ser calculada utilizando a seguinte fórmula:

Área do trapézio

Um quadrilátero plano convexo é um trapézio se, e somente se, possui dois lados paralelos, ou seja, o trapézio é um quadrilátero que possui um par de lados paralelos.

Os lados paralelos do trapézio são chamados de bases. Como as bases sempre serão diferentes, os trapézios têm então, uma base maior e uma base menor. A distância entre as bases é a altura do trapézio. Podemos classificar os trapézios de acordo com os lados não-bases em:

Isósceles – os lados não-bases são congruentes, ou seja, iguais
Escaleno – os lados não-bases não são congruentes
Retângulo – possui dois ângulos retos (90°)

Área do triângulo

A área de um triângulo é calculada utilizando as dimensões da base e altura do triângulo através da fórmula

, mas essa fórmula somente é aplicada nos triângulos em que se conhece a medida da altura. Para o cálculo da área de um triângulo qualquer podemos utilizar outras fórmulas.