Inequações do 2º grau

As inequações são expressões matemáticas que utilizam, na sua formatação, os seguintes sinais de desigualdades:

>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente


As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.

Estudo do sinal de uma função quadrática

REGRINHAS:

1- Calcular o(s) zero(s) da função.

Obs. 1. O(s) zero(s) da função são os valores de “x” que tornaram a função NULA.

2- Para verificar os valores de “x” que tornam a função positiva ou negativa, basta pegar o antecessor e o sucessor do(s) o(s) zero(s) da função e substituir em “x“ pra verificar se a função é positiva, negativa ou nula, conforme foi realizado no exemplo em sala de aula e que vocês copiaram no caderno.

3- Após a substituição, deve-se escrever os valores de “x” que tornam a função positiva, negativa ou nula.

OBS:

Y > 0 – Função POSITIVA.
Y < 0 – Função NEGATIVA.
Y = 0 – Função NULA

Valor máximo e mínimo da função quadrática

Regrinhas:
 1- Calcular o 'Xv'
2- Substituir o 'Xv' na função dada na questão para encontrar o 'YV'
3- O valor máximo ou mínimo da função quadrática será o valor do 'y'.

Coordenadas do Vértice

Zeros da Função Quadrática

y = x ² + 2x - 3
0 = x² + 2x - 3
x² + 2x - 3 = 0

∆ = b² - 4.a.c
∆ = (2)² - 4 . (1) . (-3)
∆ = 4 +12
∆ = 16

x = (-b±√∆)/2a
x= - (2) ± √16/2 . 1
x= -2 ± 4/2

x¹ = -2+4/2 = 2/2 = 1
x² = - 2 - 4/2 = -6/2 = -3

R= 1 e -3

OBS = ∆ > 0 : DOIS ZEROS DA FUNÇÃO
∆ = 0 : UMZERO DA FUNÇÃO
 ∆ < 0 : NÃO HÁ ZERO DA FUNÇÃO!

Função Quadrática

É toda função escrita na forma y = ax² + bx + c , com a diferente de zero.

Exemplo:
Determine f (5) na função f (x) = x² + 5x + 6
                   f (x) = x² + 5x + 6
                f (5) = (5)² + 5 . (5) +6
                   f (5) = 25 + 25 + 6
                        f (5) = 56

Inequação do 1º grau

inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas:
ax + b > 0;
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.

Onde a, b são números reais com a ≠ 0.

Exemplos:

-2x + 7 > 0
x – 10 ≤ 0
2x + 5 ≤ 0
12 – x < 0

Resolvendo uma inequação de 1° grau

Uma maneira simples de resolver uma equação do 1° grau é isolarmos a incógnita x em um dos membros da igualdade. Observe dois exemplos:

Exemplo1: Resolva a inequação -2x + 7 > 0.

Solução:
-2x > -7
Multiplicando por (-1)

2x < 7
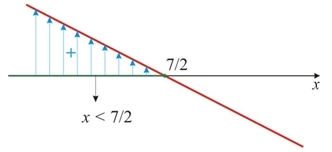
x < 7/2

Portanto a solução da inequação é x < 7/2.

Exemplo 2: Resolva a inequação 2x – 6 < 0.

Solução:
2x < 6
x < 6/2
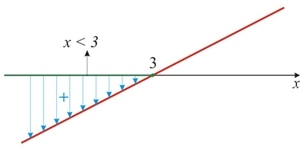
x < 3

Portanto a solução da inequação e x < 3

Pode-se resolver qualquer inequação do 1° grau por meio do estudo do sinal de uma função do 1° grau, com o seguinte procedimento:

1. Iguala-se a expressão ax + b a zero;
2. Localiza-se a raiz no eixo x;
3. Estuda-se o sinal conforme o caso.

Exemplo 1:
-2x + 7 > 0
-2x + 7 = 0
x = 7/2

Exemplo 2:
2x – 6 < 0
2x – 6 = 0
x = 3

Função do 1º grau

Zero da Função

  Denominamos zero da função o valor de x para o qual a função de x é igual a zero, ou seja, o valor de x que faz com que y seja igual a zero.

    Exemplo:

Determine o zero da função definida por y = 2x - 2

2x - 2 = 0

2x = 2

x = 2/2

x = 1

Estudo do sinal da Função

Em uma função, podemos determinar os valores reais de x que a tornam positiva, negativa ou nula.

Quando y = 0 a função será NULA

Quando y > 0 a função será POSITIVA

Quando y < 0 a função será negativa.

   

Representação gráfica de uma função afim

Função afim, linear e constante

Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é:

Função linear

Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:

Função constante

Uma função definida por f: R→R chama-se constante quando existe uma constante b R tal que f(x) = b para todo x ∈ R. A lei que define uma função constante é:

Coeficientes numéricos

Cada coeficiente numérico de uma função caracteriza um elemento do gráfico dessa função.

• Coeficiente a: coeficiente angular de uma reta. A é igual à tangente do ângulo que a reta faz com o eixo x.

Quando a > 0, a função é crescente.
Quando a < 0, a função é decrescente.

• Coeficiente b: é a ordenada do ponto em que o gráfico de f cruza o eixo das ordenadas, ou seja, b = f(0).

Domínio, contradomínio, conjunto imagem e valor de uma função

O domínio contém todos os elementos x para os quais a função deve ser definida. Já o contradomínio é o conjunto que contém os elementos que podem ser relacionados a elementos do domínio. Define-se imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.

Função x Relação

Uma função é uma relação entre duas variáveis x e y tal que o conjunto de valores para x é determinado, e a cada valor x está associado um e somente um valor para y.

*A relação é expressa por y = f(x).
*O conjunto de valores de x é dito domínio da função.
*As variáveis x e y são ditas, respectivamente, independente e dependente.

Equações irracionais

Regrinhas:

1- Para resolver uma equação irracional devemos elevar os dois membros da equação ao valor semelhante ao indíce do radical da equação. Após isso aplicamos as propriedades de radiciação e potenciação para eliminar o radical e resolver a questão.

2- Ao final da resolução devemos escrever o conjunto verdade.