Blog destinado a divulgar diversos assuntos interessantes da Matemática. Problemas, exercícios, vídeos, imagens e tudo mais nesse blog.
20/11/2012
MULTIPLICAÇÃO DE FRAÇÕES ALGÉBRICAS
As multiplicações de frações algébricas devem ser calculadas da mesma mesma de uma fração fracionária.
ADIÇÃO E SUBTRAÇÃO DE FRAÇÕES ALGÉBRICAS
Na adição e subtração deve ser calculada da mesma maneira de uma fração fracionária. Obtém-se frações equivalentes e de mesmo denominador; o denominador comum poderá ser o produto ou o mmc dos denominadores; somamos ou subtraímos os numeradores e conservamos o denominador comum.

MDC E MMC
O MMC de dois números naturais é o produto dos fatores comuns e não-comuns, cada um com seu maior expoente.
O MDC de dois números naturais é o produto dos fatores comuns, cada um com seu menor expoente.

.jpg)

O MDC de dois números naturais é o produto dos fatores comuns, cada um com seu menor expoente.

.jpg)

SIMPLIFICAÇÃO DE FRAÇÕES ALGÉBRICAS
Para simplificar uma fração algébrica, devemos dividir os seus termos por um divisor comum diferente de zero, a fim de obter uma fração equivalente mais simples.
EXEMPLOS:
EXEMPLOS:
FRAÇÕES ALGÉBRICAS
O quociente de dois polinômios escritos na forma fracionária, com uma ou mais variáveis ou incógnitas no denominador (diferente de zero), chama-se fração algébrica.
EXEMPLOS:



EXEMPLOS:


SOMA OU DIFERENÇA DE CUBOS
a³+b³ = (a+b) . ( a²-ab+b²)
a³+27 = (a+3) . (a²-a.3+3²) = (a+3) . (a²-3a+9)

REGRAS:
1ª- Tirar a raíz cúbica dos termos fatorados.
2ª- Verificar o sinal do primeiro polinômio que será multiplicado.
3ª- O primeiro polinômio que vamos colocar ou que ficará dentro dos parênteses vai ser a soma ou a diferença dos termos que foram calculados na regra 1.
4ª- Multiplicar esse polinômio pelo:
* quadrado do primeiro menos o primeiro vezes o segundo mais o quadrado do segundo (soma de cubos).
* quadrado do primeiro mais o primeiro vezes o segundo mais o quadrado do segundo (diferença de cubos).
5ª- Simplificar o polinômio e escrever a resposta final corretamente para poder acertar a questão e tirar uma nota boa na prova de matemática.
a³+27 = (a+3) . (a²-a.3+3²) = (a+3) . (a²-3a+9)

REGRAS:
1ª- Tirar a raíz cúbica dos termos fatorados.
2ª- Verificar o sinal do primeiro polinômio que será multiplicado.
3ª- O primeiro polinômio que vamos colocar ou que ficará dentro dos parênteses vai ser a soma ou a diferença dos termos que foram calculados na regra 1.
4ª- Multiplicar esse polinômio pelo:
* quadrado do primeiro menos o primeiro vezes o segundo mais o quadrado do segundo (soma de cubos).
* quadrado do primeiro mais o primeiro vezes o segundo mais o quadrado do segundo (diferença de cubos).
5ª- Simplificar o polinômio e escrever a resposta final corretamente para poder acertar a questão e tirar uma nota boa na prova de matemática.
FATORAÇÃO POR AGRUPAMENTO
O processo de agrupamento é utilizado quando a expressão a ser fatorada apresenta grupos de termos com fatores comuns.
EXEMPLOS:
ax + bx + ay + by= 3a + ab - 6y - 2by=
x (a+b) + y ( a+b )= a (3+b) -2y (3+b)=
(a+b) . (x+y) (3+b), (a-2y)
REGRAS:
1ª- Observara expressão e identificar os termos semelhantes.
2ª- Organizar a expressão colocando os termos semelhantes juntos.
3ª- Colocar o fator comum em evidência.
4ª- Dividir o termo da expressão pelo fatorem evidência e colocar o resultado dentro dos parênteses.
5ª- Multiplicar os termos que estão dentro dos parênteses pela soma dos fatores externos.

EXEMPLOS:
ax + bx + ay + by= 3a + ab - 6y - 2by=
x (a+b) + y ( a+b )= a (3+b) -2y (3+b)=
(a+b) . (x+y) (3+b), (a-2y)
REGRAS:
1ª- Observara expressão e identificar os termos semelhantes.
2ª- Organizar a expressão colocando os termos semelhantes juntos.
3ª- Colocar o fator comum em evidência.
4ª- Dividir o termo da expressão pelo fatorem evidência e colocar o resultado dentro dos parênteses.
5ª- Multiplicar os termos que estão dentro dos parênteses pela soma dos fatores externos.

FATORAÇÃO
Fatorar um número é escrevê-lo em forma de um produto de dois ou mais números.
1º caso:


.jpg)
2º caso: fator comum em evidência ... :
3x+6= a²+a=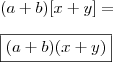
3 (x+2) a (a+1)
Regras:
1ª- Analisar o polinômio e identificar o maior número que pode dividir todos os termos.
2ª- Escrever esse número, colocando-o como fator externo.
3ª- Efetuar a divisão de todos termos do polinômio pelo número ( fator externo ).
4ª- Escrever o resultado da divisão dentro dos parênteses do lado do fator externo.
1º caso:


.jpg)
2º caso: fator comum em evidência ... :
3x+6= a²+a=
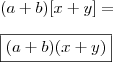
3 (x+2) a (a+1)
Regras:
1ª- Analisar o polinômio e identificar o maior número que pode dividir todos os termos.
2ª- Escrever esse número, colocando-o como fator externo.
3ª- Efetuar a divisão de todos termos do polinômio pelo número ( fator externo ).
4ª- Escrever o resultado da divisão dentro dos parênteses do lado do fator externo.
APRESENTAÇÃO
Blog feito pelas alunas do 8º ano ( 7ª série ) do turno vespertino da disciplina de Matemática do Centro Educacional Objetivo ( CEOB ) . Trabalho solicitado pelo professor de Matemática Anderson Macedo.
Componentes :
Danielle Barbosa ;
Márcya Ellen ;
Islany Oliveira ;
Gabriella Reis ;
Keilane Carmo ;
Maria Luíza !
Componentes :
Danielle Barbosa ;
Márcya Ellen ;
Islany Oliveira ;
Gabriella Reis ;
Keilane Carmo ;
Maria Luíza !
Assinar:
Comentários (Atom)